
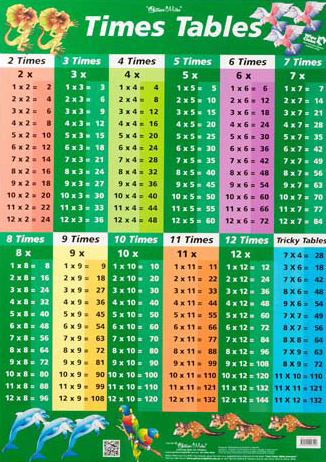
If I want to know that exactly, then I reach for Mathematica (or if I absolutely have to, I reach for pencil and paper to apply multiplication in columns). This might make a case for drawing the line higher. You can’t manage on less, and more is of no use.ģ) But there is another useful algorithm, which is approximating numbers to a few significant digits. If this was the only consideration, we have a clear argument for where to draw our line-at the 10 times table. Knowledge of 11 and 12 times tables is completely irrelevant. By definition it needs the 0–9 times tables (and implicitly understanding the 10 times table), since it only takes one digit at a time, but any single digit could come up. The question is where.Ģ) There are many fancy computation algorithms, but most of us learn “multiplying in columns,” which involves operating on one digit at a time while managing number place and carrying overflows on to the next column.

We must draw a line somewhere and then move to a more algorithmic approach. This, after all, is why math was invented, so that we don’t have to know the answers to all possible calculations, but instead have a way to work them out when needed. “Knowing” the answer to all possible questions is a big task and not worth the effort. What’s so special about multiplying 1 to 12? Why stop at the 12 times table-why not learn 13, 14, 15, 16, and 17 times tables? Why not learn your 39 times table? As the table number goes up, the amount to learn increases as a square of the number while the commonality of encountering a problem that uses that table goes down. But knowing ANY answer to ANY question is useful. There are lots of small multiplication problems in day-to-day life, and there is no doubt that knowing the answer to these is useful. I am going to claim that there are three basic reasons:ġ) To directly know the answer to common multiplication questions.ġ) This reason is important. Let’s start with a basic question: exactly why do we use times tables at all? (This is the kind of question my work on has me asking a lot!) To find it being given new emphasis nearly 40 years later struck me as so odd that I thought I should investigate it a little more mathematically. Since that madness ended with decimalization the year after I was born, by the late 1970s when I had to learn my 12 times table, it already seemed to be an anachronistic waste of time. Now, I always believed that the reason why I learned my 12 times table was because of the money system that the UK used to have-12 pennies in a shilling. My government (I’m in the UK) recently said that children here should learn up to their 12 times table by the age of 9.


 0 kommentar(er)
0 kommentar(er)
